Did Time Start at the Big Bang?

Leonard Susskind on Quantum Information, Quantum Gravity, and Holography

Albert Einstein: Who Revolutionized Physics

Albert Einstein was a German-born theoretical physicist, best known for his Special and General Theory of Relativity and the concept of mass-energy equivalence expressed by the famous equation, E = mc². He received the Nobel Prize in Physics in 1921 “for his services to theoretical physics, and especially for his discovery of the law of the photoelectric effect” and he made some essential contributions to the early development of quantum theory. He was named “Person of the Century” by Time magazine in 1999, the fourth most admired person of the 20th Century according to a 1999 Gallup poll, and “the greatest scientist of the twentieth century and one of the supreme intellects of all time” according to “The 100: A Ranking of the Most Influential Persons in History” in 1978.

Albert Einstein was born into a non-practising Jewish family in Ulm in the Kingdom of Württemberg, Germany on 14 March 1879. He was always a little different from other children: his head was slightly larger than normal, and he hardly spoke as a young boy, leading one housekeeper to consider him “retarded”. At an early age, his family moved to Munich where Einstein attended a Catholic school and showed an early aptitude for mathematics, particularly geometry and calculus (although he disliked the school’s policy of strict memorization, which he thought unhelpful). Outside of school, he explored his own path of learning in mathematics and philosophy with a medical student and friend of the family, Max Talmud.

At 15, after his father’s electrical equipment business failed, he followed his family to Pavia, Italy (not wishing to stay and finish his schooling in Germany), and then on to Aarau, Switzerland, where he finally finished high school. At the age of just 16, he had already made his first conceptual breakthrough while looking at a mirror and wondering what he would see if he were traveling at the speed of light (a thought experiment sometimes referred to as “Einstein’s Mirror”). In 1896, he renounced his German citizenship in order to avoid military service, and went to study mathematics and physics at the Swiss Federal Institute of Technology in Zürich, graduating in 1900. He gained Swiss citizenship in 1901 and never revoked it.

Unable to find a teaching post after graduation, Einstein eventually obtained a job evaluating patent applications for electromagnetic devices at the Swiss patent office in Bern. He married a Serb woman named Mileva Maric in 1903, and the couple were to bear two sons, Hans Albert (1904) and Eduard (1910), (and possibly another child, Lieserl, before their marriage, who either died in childhood or was put up for adoption), before divorcing in 1919.

In 1905, sometimes referred to as his “annus mirabilis” (wonderful year), and while he was still working in the patent office, the young 26 year old Einstein completed his PhD (with a thesis on “A new determination of molecular dimensions”) and had no less than four important papers published in the “Annalen der Physik”, the leading German physics journal:

• a paper on the particulate nature of light, in which he explained the “photoelectric effect” and certain other experimental results by proposing that light interacts with matter as discrete “packets” or quanta of energy, rather than as a wave (an idea first suggested by Max Planck as a purely mathematical manipulation).
• a paper explaining Brownian motion (the seemingly random movement of particles suspended in a fluid) as direct evidence of molecular action, thus supporting the atomic theory (that all matter is made up of tiny atoms and molecules).
• a paper, which has become known as the Special Theory of Relativity, on the electrodynamics of moving bodies, which showed that the speed of light is independent of the observer’s state of motion, and introduced the idea that the space-time frame of a moving body could slow down and contract in the direction of motion relative to the frame of the observer.
• a paper on mass-energy equivalence, in which he deduced the famous equation E = mc² from his special relativity equations, suggesting that tiny amounts of mass could be converted into huge amounts of energy (which presaged the later development of nuclear power).

Much of this work was highly controversial (or just ignored) within the scientific community of the time, and he continued his work at the patent office until 1908. But he had earned his PhD from the University of Zürich in 1905, and he was eventually able to obtain a privatdozent position at the University of Bern in 1908, followed by brief teaching posts at the University of Zürich and the University of Prague in 1911.

During this time he continued to publish papers, but it was only on moving back to the Swiss Federal Institute of Technology in Zürich in 1912 that he began working in earnest on a generalization of his theory of relativity. He benefitted from the mathematical assistance of his old friend Marcel Grossman, who was one of the only people in Zurich with whom Einstein could discuss his new ideas. He moved on to Berlin in 1914 (at the personal request of Max Planck), where he became a member of the Prussian Academy of Sciences, a director of the Kaiser Wilhelm Institute for Physics and a professor at the Humboldt University of Berlin, as well as maintaining an ongoing relationship with Leiden University in the Netherlands (through his contacts there with the physicists Hendrik Lorentz and Willem de Sitter). He became actively involved in anti-war demonstrations during World War I, publicly advocating civil disobedience and the refusal of conscription.

Einstein gave a series of lectures in 1915 about his new theory, which was to become known as the General Theory of Relativity, including a new equation to replace Newton’s law of gravity, now known as Einstein’s field equation. The complete theory was finally published in 1916, although physicists and mathematicians like Karl Schwarzschild and Ludwig Flamm were starting to publish solutions to his field equations even before its publication. General relativity is based on the notion that gravity and acceleration are indistinguishable (the principle of equivalence) and describes gravity as a property of the geometry (or, more specifically, the warpage) of space-time, leading to the prediction of phenomena like the bending of light, black holes and wormholes.

A year later, Einstein published a paper introducing a new notion into his General Theory of Relativity, a sort of anti-gravity force which he called the “cosmological constant” that kept the universe from collapsing in on itself, in an attempt to model the behavior of the entire universe, while retaining his firm belief in a Newtonian infinite, static model of the universe. He later called this idea his “greatest blunder” although, in the light of recent discoveries about the accelerating universe and dark energy, it is beginning to look remarkably prescient.

He divorced Mileva Maric in 1919, having lived apart for the last five years, and within months of the divorce, married his cousin Elsa Löwenthal (who had nursed him through an illness) and together they raised Margot and Ilse, Elsa’s daughters from her first marriage.

Despite the attempts by many scientists to disprove the General Theory of Relativity, the British astronomer Arthur Eddington claimed in 1919 to have confirmed Einstein’s prediction of the gravitational deflection of starlight by the Sun, leading, almost overnight, to global renown and international media attention for Einstein. His fellow scientists began to speak of general relativityin terms such as “probably the greatest scientific discovery ever made” and “the greatest feat of human thinking about nature”. He was awarded the 1921 Nobel Prize in Physics, “for his services to theoretical physics, and especially for his discovery of the law of the photoelectric effect” (i.e. not for his theory of relativity).

The Birch and Swinnerton-Dyer Conjecture

Elliptic curves have a long and distinguished history that can be traced back to antiquity. They are prevalent in many branches of modern mathematics, foremost of which is number theory.

In simplest terms, one can describe these curves by using a cubic equation of the form

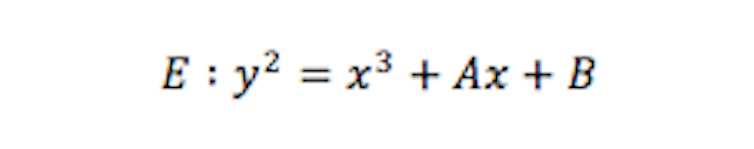
where A and B are fixed rational numbers (to ensure the curve E is nice and smooth everywhere, one also needs to assume that its discriminant 4A³ + 27B² is non-zero).

To illustrate, let’s consider an example: choosing A=-1 and B=0, we obtain the following picture:

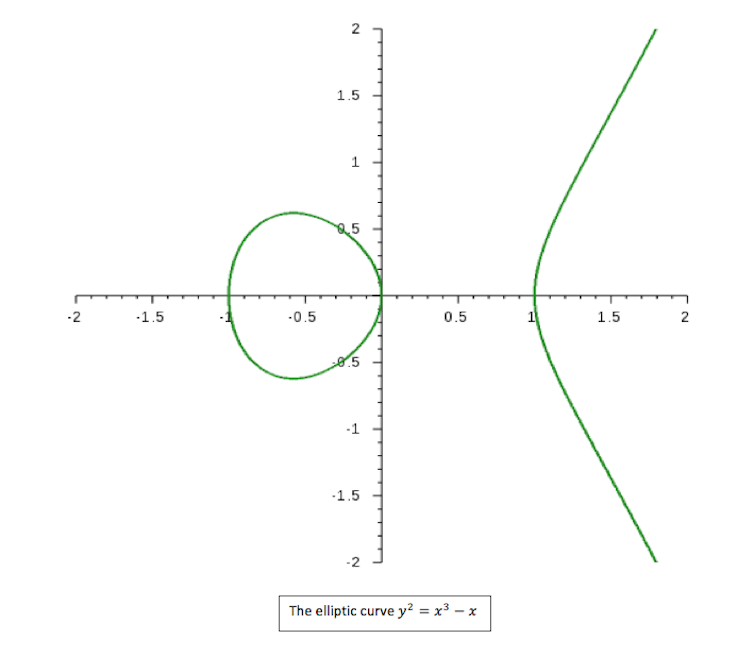
At this point it becomes clear that, despite their name, elliptic curves have nothing whatsoever to do with ellipses! The reason for this historical confusion is that these curves have a strong connection to elliptic integrals, which arise when describing the motion of planetary bodies in space.

The ancient Greek mathematician Diophantus is considered by many to be the father of algebra. His major mathematical work was written up in the tome Arithmetica which was essentially a school textbook for geniuses. Within it, he outlined many tools for studying solutions to polynomial equations with several variables, termed Diophantine Equations in his honour.

One of the main problems Diophantus considered was to find all solutions to a particular polynomial equation that lie in the field of rational numbers Q. For equations of “degree two” (circles, ellipses, parabolas, hyperbolas) we now have a complete answer to this problem. This answer is thanks to the late German mathematician Helmut Hasse, and allows one to find all such points, should they exist at all.

Returning to our elliptic curve E, the analogous problem is to find all the rational solutions (x,y) which satisfy the equation defining E. If we call this set of points E(Q), then we are asking if there exists an algorithm that allows us to obtain all points (x,y) belonging to E(Q).

At this juncture we need to introduce a group law on E, which gives an eccentric way of fusing together two points (p₁ and p₂) on the curve, to obtain a brand new point (p₄). This mimics the addition law for numbers we learn from childhood (i.e. the sum or difference of any two numbers is still a number). There’s an illustration of this rule below:

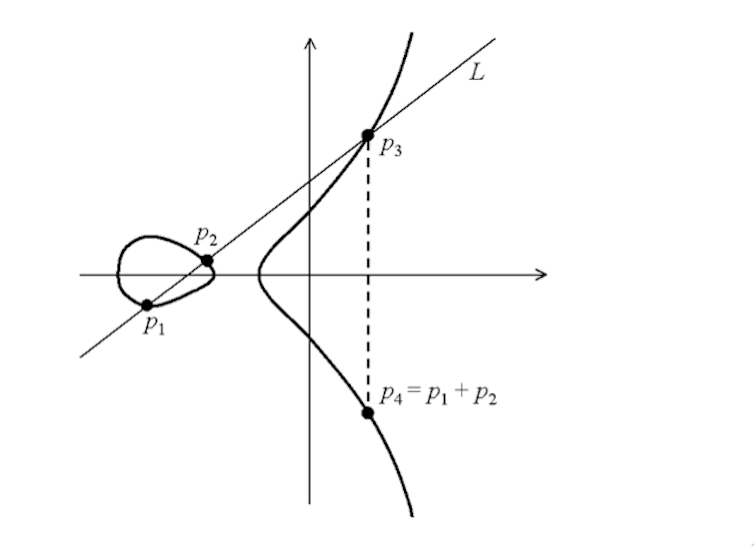
Under this geometric model, the point p₄ is defined to be the sum of p₁ and p₂ (it’s easy to see that the addition law does not depend on the order of the points p₁, p₂). Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.

Louis Mordell, who was Sadleirian Professor of Pure Mathematics at Cambridge University from 1945 to 1953, was the first to determine the structure of this group of rational points. In 1922 he proved

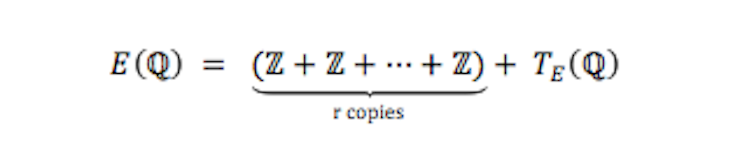
where the number of copies of the integers Z above is called the “rank r(E) of the elliptic curve E”. The finite group Τ_E(Q) on the end is uninteresting, as it never has more than 16 elements.

i want to thank conversation, most of the content the in  this series  is designed with help of their series check herehttps://theconversation.com/millennium-prize-the-birch-and-swinnerton-dyer-conjecture-4242

Navier–Stokes Equation

The equations

In order to understand the Navier-Stokes equations and their derivation we need considerable mathematical training and also a sound understanding of basic physics.

Without that, we must draw upon some very simple basics and talk in terms of broad generalities – but that should be sufficient to give the reader a sense of how we arrive at these fundamental equations, and the importance of the questions.

From this point, I’ll refer to the Navier-Stokes equations as “the equations”.

The equations governing the motion of a fluid are most simply described as a statement of Newton’s Second Law of Motion as it applies to the movement of a mass of fluid (whether that be air, water or a more exotic fluid). Newton’s second law states that:

Mass x Acceleration = Force acting on a body

For a fluid the “mass” is the mass of the fluid body; the “acceleration” is the acceleration of a particular fluid particle; the “forces acting on the body” are the total forces acting on our fluid.

Without going into full details, it’s possible to state here that Newton’s Second Law produces a system of differential equations relating rates of change of fluid velocity to the forces acting on the fluid. We require one other physical constraint to be applied on our fluid, which can be most simply stated as:

Mass is conserved! – i.e. fluid neither appears nor disappears from our system.

The solution

Having a sense of what the Navier-Stokes equations are allows us to discuss why the Millennium Prize solution is so important. The prize problem can be broken into two parts. The first focuses on the existence of solutions to the equations. The second focuses on whether these solutions are bounded (remain finite).

It’s not possible to give a precise mathematical description of these two components so I’ll try to place the two parts of the problem in a physical context.

1) For a mathematical model, however complicated, to represent the physical world we are trying to understand, the model must first have solutions.

At first glance, this seems a slightly strange statement – why study equations if we are not sure they have solutions? In practice we know many solutions that provide excellent agreement with many physically relevant and important fluid flows.

But these solutions are approximations to the solutions of the full Navier-Stokes equations (the approximation comes about because there is, usually, no simple mathematical formulae available – we must resort to solving the equations on a computer using numerical approximations).

Although we are very confident that our (approximate) solutions are correct, a formal mathematical proof of the existence of solutions is lacking. That provides the first part of the Millennium Prize challenge.

2) The second part asks whether the solutions of the Navier-Stokes equations can become singular (or grow without limit).

Again, a lot of mathematics is required to explain this. But we can examine why this is an important question.

There is an old saying that “nature abhors a vacuum”. This has a modern parallel in the assertion by physicist Stephen Hawking, while referring to black holes, that “nature abhors a naked singularity”. Singularity, in this case, refers to the point at which the gravitational forces – pulling objects towards a black hole – appear (according to our current theories) to become infinite.

In the context of the Navier-Stokes equations, and our belief that they describe the movement of fluids under a wide range of conditions, a singularity would indicate we might have missed some important, as yet unknown, physics. Why? Because mathematics doesn’t deal in infinites.

The history of fluid mechanics is peppered with solutions of simplified versions of the Navier-Stokes equations that yield singular solutions. In such cases, the singular solutions have often hinted at some new physics previously not considered in the simplified models.

Identifying this new physics has allowed researchers to further refine their mathematical models and so improve the agreement between model and reality.

If, as many believe, the Navier-Stokes equations do posses singular solutions then perhaps the next Millennium Prize will go to the person that discovers just what new physics is required to remove the singularity.

Then nature can, as all fluid mechanists already do, come to delight in the equations handed down to us by Claude-Louis Navier and George Gabriel Stokes.

Yang–Mills and Mass Gap

Many field theories fall into a class called gauge field theories, where a particular collection of symmetries, called the gauge group, acts on the fields and particles. In the case that these symmetries all commute, so-called abelian gauge theories, we have a reasonable understanding of the quantization.

This includes the case of the electromagnetic field, quantum electrodynamics, for which the theory makes impressively accurate predictions.

The first example of a non-abelian theory that arose historically is the theory of the electro-weak interaction, which requires a mechanism to make the predicted particles massive as we observe them in nature. This involves the so-called Higgs boson, which is currently being searched for with the Large Hadron Collider (LHC) at CERN.

The notable feature of this theory for our present discussion is that the Higgs mechanism is classical and carries over to the quantum theory under the quantization process.

The case of interest in the Millennium Problem “Yang-Mills theory and Mass-Gap” is Yang-Mills gauge theory, a non-abelian theory which we expect to describe quarks and the strong force that binds the nucleus and powers the sun. Here we encounter a contradiction between the classical and quantum theories.

The classical theory predicts massless particles and long-range forces. The quantum theory has to match the real world with short-range forces and massive particles. Physicists expect various mathematical properties such as the “mass gap” and “asymptotic freedom” to explain the non-existence of massless particles in observations of the strong interactions.

As these properties are not visible in the classical theory and arise only in the quantum theory, understanding them means we need a rigorous approach to “quantum Yang-Mills theory”. Currently we do not have the mathematics to do this, although various approximations and simplifications can be done which suggest the quantum theory has the required properties.

Hodge conjecture

It states :-
the algebraic topology of a non-singular complex algebraic variety to its subvarieties. More specifically, the conjecture states that certain de Rham cohomology classes are algebraic, that is, they are sums of Poincaré duals of the homology classes of subvarieties. It was formulated by the Scottish mathematician William Vallance Douglas Hodge as a result of a work in between 1930 and 1940 to enrich the description of de Rham cohomology to include extra structure that is present in the case of complex algebraic varieties. It received little attention before Hodge presented it in an address during the 1950 International Congress of Mathematicians, held in Cambridge, Massachusetts.

Statement of the Hodge conjecture

We call this the group of Hodge classes of degree 2k on X.

The modern statement of the Hodge conjecture is:Hodge conjecture. Let X be a non-singular complex projective manifold. Then every Hodge class on X is a linear combination with rational coefficients of the cohomology classes of complex subvarieties of X.

A projective complex manifold is a complex manifold which can be embedded in complex projective space. Because projective space carries a Kähler metric, the Fubini–Study metric, such a manifold is always a Kähler manifold. By Chow’s theorem, a projective complex manifold is also a smooth projective algebraic variety, that is, it is the zero set of a collection of homogeneous polynomials.

The Poincaré conjecture

Here Comes  Donuts

A good way to visualise Poincaré’s conjecture is to examine the boundary of a ball (a two-dimensional sphere) and the boundary of a donut (called a torus). Any loop of string on a 2-sphere can be shrunk to a point while keeping it on the sphere, whereas if a loop goes around the hole in the donut, it cannot be shrunk without leaving the surface of the donut.

Some typical mathematical language

In mathematics, the Poincaré conjecture  is a theoremabout the characterization of the 3-sphere, which is the hypersphere that bounds the unit ball in four-dimensional space.

The conjecture states: – Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere

Poincaré’s question and a little bit History

At the beginning of the 20th century, Henri Poincaré was working on the foundations of topology—what would later be called combinatorial topology and then algebraic topology. He was particularly interested in what topological properties characterized a  sphere.

 Poincaré wondered whether a 3-manifold with the homology of a 3-sphere and also trivial fundamental group had to be a 3-sphere. Poincaré’s new condition—i.e., “trivial fundamental group”—can be restated as “every loop can be shrunk to a point.”

The original phrasing was as follows:

Consider a compact 3-dimensional manifold V without boundary. Is it possible that the fundamental group of V could be trivial, even though V is not homeomorphic to the 3-dimensional sphere?

Here comes Perelmen

Hamilton’s program and Perelman’s solution

Hamilton’s program was started in his 1982 paper in which he introduced the Ricci flow on a manifold and showed how to use it to prove some special cases of the Poincaré conjecture. In the following years he extended this work, but was unable to prove the conjecture. The actual solution was not found until Grigori Perelman published his papers.

In late 2002 and 2003 Perelman posted three papers on the arXiv. In these papers he sketched a proof of the Poincaré conjecture and a more general conjecture, Thurston’s geometrization conjecture, completing the Ricci flow program outlined earlier by Richard S. Hamilton.

Beauty Of Mathematics Do Not Need money or Medals

Perelman was awarded both a Fields medal (the mathematical equivalent of a Nobel prize) and also offered a million dollars for solving one of the Millenium prizes from the Clay Institute.

He turned down both these awards, preferring to live a quiet life in St Petersburg.

Clay Mathematics Institute Millennium Problems

The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute on May 24, 2000.  In which only poincare conjecture  has been solved by russian mathematician Grigori Perelman.

Yang–Mills and Mass Gap

Experiment and computer simulations suggest the existence of a “mass gap” in the solution to the quantum versions of the Yang-Mills equations. But no proof of this property is known.

Riemann Hypothesis

The prime number theorem determines the average distribution of the primes. The Riemann hypothesis tells us about the deviation from the average. Formulated in Riemann’s 1859 paper, it asserts that all the ‘non-obvious’ zeros of the zeta function are complex numbers with real part 1/2.

P vs NP Problem

If it is easy to check that a solution to a problem is correct, is it also easy to solve the problem? This is the essence of the P vs NP question. Typical of the NP problems is that of the Hamiltonian Path Problem: given N cities to visit, how can one do this without visiting a city twice? If you give me a solution, I can easily check that it is correct. But I cannot so easily find a solution.

Navier–Stokes Equation

This is the equation which governs the flow of fluids such as water and air. However, there is no proof for the most basic questions one can ask: do solutions exist, and are they unique? Why ask for a proof? Because a proof gives not only certitude, but also understanding.

Hodge Conjecture

The answer to this conjecture determines how much of the topology of the solution set of a system of algebraic equations can be defined in terms of further algebraic equations. The Hodge conjecture is known in certain special cases, e.g., when the solution set has dimension less than four. But in dimension four it is unknown.

Poincaré Conjecture

In 1904 the French mathematician Henri Poincaré asked if the three dimensional sphere is characterized as the unique simply connected three manifold. This question, the Poincaré conjecture, was a special case of Thurston’s geometrization conjecture. Perelman’s proof tells us that every three manifold is built from a set of standard pieces, each with one of eight well-understood geometries.

Birch and Swinnerton-Dyer Conjecture

Supported by much experimental evidence, this conjecture relates the number of points on an elliptic curve mod p to the rank of the group of rational points. Elliptic curves, defined by cubic equations in two variables, are fundamental mathematical objects that arise in many areas: Wiles’ proof of the Fermat Conjecture, factorization of numbers into primes, and cryptography, to name three.

we will go through every problem in detail in upcoming posts specially reimann ,poincare and P vs NP problem